Category Theory for Programmers: Exercises (Chapter 1)

1. Implement the identity function.

const identity = <T = any>(x: T) => x;

2. Implement the composition function.

const compose = <T, U, V>(f: (x: U) => V, g: (x: T) => U) => {
    return (x: T) => f(g(x));
};

3. Write a program that tries to test that your composition function respects identity.

const respectsIdentity = (f: (x: any) => any, x: any) => {
    return compose(f, identity)(x) === compose(identity, f)(x);
};

// e.g.
respectsIdentity((n: number) => (!(n % 2) ? 'Even' : 'Odd'), 12) === true;

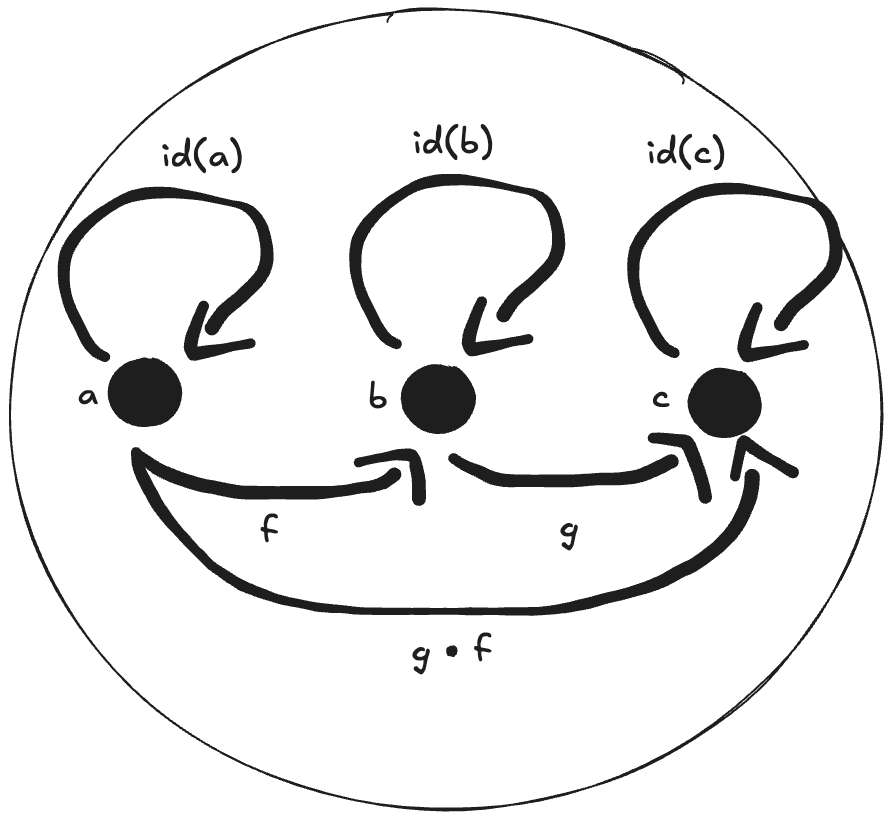
4. Is the world-wide web a category in any sense? Are links morphisms?

In a sense:

Links to the current page: id(a), id(b) and id(c)
A link from a first page to a second page: f
A link from the second page to a third page: g
A link from the first page to the third page: g . f

Although there won’t necessarily be a link from the first to the third page, so the web is a category only insofar as there is.

Simple category

5. Is Facebook a category, with people as objects and friendships as morphisms?

No, and in a partial sense less so than in the web example:

There are no identity arrows if we say a person cannot be friends with themselves even by composition (would this be valid?)
There is no necessary composition since there can be an arrow between person A and person B, another between person B and person C, but there may not be an arrow between person A and person C

6. When is a directed graph a category?

When it has loops and is transitive:

Transitive graph with loops