Natural Transformations

1. Define a natural transformation from the Maybe functor to the list functor. Prove the naturality condition for it.

-- Natural transformation:
alpha :: Maybe a -> [a]
alpha Nothing = []
alpha (Just x) = [x] 

-- Naturality condition (NC):
fmap f . alpha = alpha . fmap f

-- NC demonstrated for Nothing: 
fmap f (alpha Nothing) = fmap f [] = []
alpha (fmap f Nothing) = alpha Nothing = []

-- NC demonstrated for Just x:
fmap f (alpha (Just x)) = fmap f (x:xs) = f x : fmap f [] = [f x]
alpha (fmap f (Just x)) = alpha (Just (f x)) = [f x]

2. Define at least two different natural transformations between Reader () and the list functor. How many different lists of () are there?

alpha :: Reader () a -> [a]
alpha (Reader _) = [] 
-- Or:
alpha (Reader g) = [g ()] 

The List () type has two members: Nil and Cons a (List a). These correspond to the two only possible implementations of alpha shown above, where [] is the same as Nil and [g ()] is a function from () returning a value of type a.

3. Continue the previous exercise with Reader Bool and Maybe.

alpha :: Reader Bool a -> Maybe a
alpha (Reader _) = Nothing
-- Or:
alpha (Reader g) = Just (g True)
-- Or:
alpha (Reader g) = Just (g False)

The elements of Maybe Bool are Just True, Just False and Nothing. These are in correspondence with the three possible alpha functions defined above.

4. Show that the horizontal composition of natural transformation satisfies the naturality condition (hint: use components). It’s a good exercise in diagram chasing.

The naturality condition to satisfy here is:

G'(F' h) · (β ◦ α)a = (β ◦ α)b · G(F h)

This is shown by diagram chasing (following the relevant arrows):

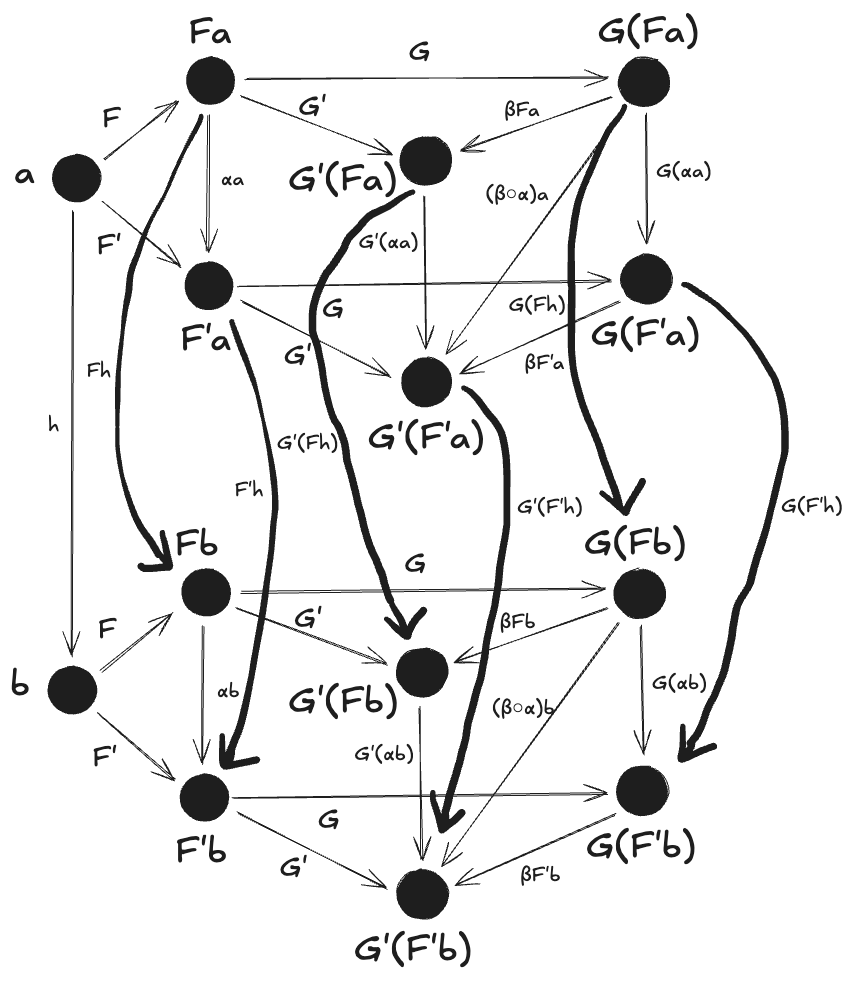
6. Create a few test cases for the opposite naturality condition of transformations between different Op functors:

Op Int -> Op Bool

A test case using listToBool for the natural transformation, tail as the first argument to contramap and head as the f parameter to Op:

listToBool (Op f) = Op (\x -> f x > 0)

The “opposite” naturality condition:

contramap tail . listToBool = listToBool . contramap tail

   contramap tail (listToBool (Op head))
=> contramap tail (Op (\x -> head x > 0))
=> Op ((\x -> head x > 0) . tail)

   listToBool (contramap tail (Op head))
=> listToBool (Op (head . tail))
=> Op (\x -> (head . tail) x > 0)

Op Bool -> Op String

A test case using predToStr from Milewski’s blog for the natural transformation, isEvenLength as the first argument to contramap and not for the f parameter to Op:

predToStr (Op f) = Op (\x -> if f x then "T" else "F")

isEvenLength :: String -> Bool
isEvenLength = iseven . length

The “opposite” naturality condition:

contramap isEvenLength . predToStr = predToStr . contramap isEvenLength

   contramap isEvenLength (predToStr (Op not))
=> contramap isEvenLength (Op (\x -> if not x then "T" else "F"))
=> Op ((\x -> if not x then "T" else "F") . isEvenLength)

   predToStr (contramap isEvenLength (Op not))
=> predToStr (Op (not . isEvenLength))
=> Op (\x -> if (not . isEvenLength) x then "T" else "F")