Category Theory for Programmers: Exercises (Chapter 2)
1. Define a higher-order function memoize that takes a pure function as an argument and calls it once for every argument, stores the result internally and returns it for subsequent calls with the same argument.
const memoize = <T extends string | number, U>(fn: (x: T) => U) => {
const seen = {} as Record<T, U>;
return (x: T) => {
if (seen[x] === undefined) seen[x] = fn(x);
return seen[x];
};
};
const returnNum = memoize((n: number) => {
for (let i = 0; i < 1_000_000_000; i++) {}
return n;
});
console.time('2');
returnNum(2);
console.timeEnd('2');
console.time('2');
returnNum(2);
console.timeEnd('2');
console.time('7');
returnNum(7);
console.timeEnd('7');
console.time('7');
returnNum(7);
console.timeEnd('7');
/**
* 2: 466.089ms
* 2: 0.002ms
* 7: 466.118ms
* 7: 0.001ms
**/
2/3. Memoize a function that produces random numbers. Does it work?
It creates a pure function where the domain is mapped to the codomain at random.
const getRandomInt = memoize((max: number) => {
return Math.floor(Math.random() * max);
});
for (let i = 0; i < 3; i++) {
console.log(getRandomInt(3));
console.log(getRandomInt(4));
}
/**
* 0
* 1
* 0
* 1
* 0
* 1
**/
4. Which of these C++ functions are pure?
(a) A factorial function: Ordinary example of a mathematical function.
(b) std::getChar: Typical example of an non-mathematical function. The output comes “from the world” rather than from a mapping of input to output.
(c) bool f() { std::cout << "Hello" << std::endl; return true; }: Sending output to the console is a side effect, so this is not a pure function even though it returns the same result each it is called.
(d) int f(int x) { static int y = 0; y += x; return y; }: Simple mathematical function using integers for the domain and codomain.
5. How many different functions are there from Bool to Bool? Can you implement them all?
2 possible inputs x 2 possible outputs = 4 functions:
(_: true) => true;
(_: true) => false;
(_: false) => true;
(_: false) => false;
6. Draw a picture of a category whose only objects are the types Void, () (unit), and Bool; with arrows corresponding to all possible functions between these types. Label the arrows with the names of the functions.
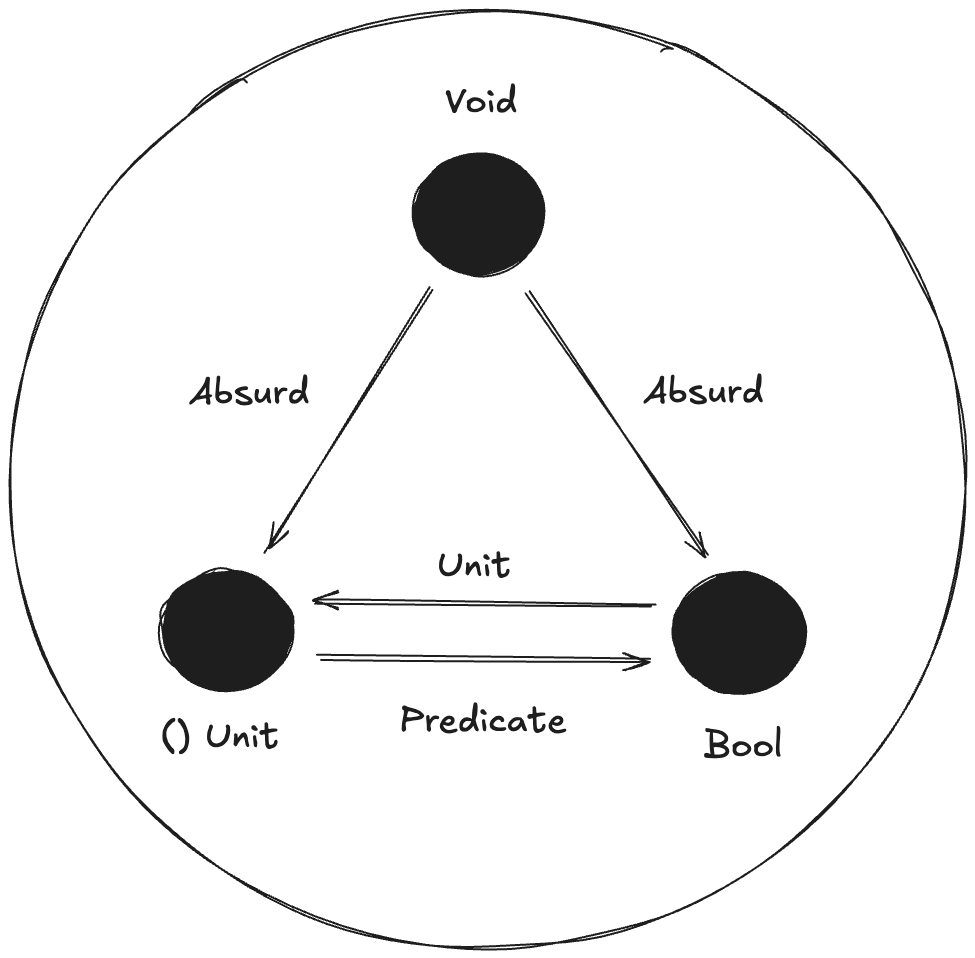
- Functions from an empty set (Void) can never be called.
- Functions to Booleans are predicates.
- Functions to a singleton set (Unit) are generically termed Unit.
- Functions to Void would be empty functions but these are invalid in Haskell and not described in this chapter.