Category Theory for Programmers: Exercises (Chapter 3)

Categories Great and Small

1. Generate a free category from: (a) A graph with one node and no edges (b) A graph with one node and one (directed) edge (hint: this edge can be composed with itself) (c) A graph with two nodes and a single arrow between them (d) A graph with a single node and 26 arrows marked with the letters of the alphabet: a, b, c … z.

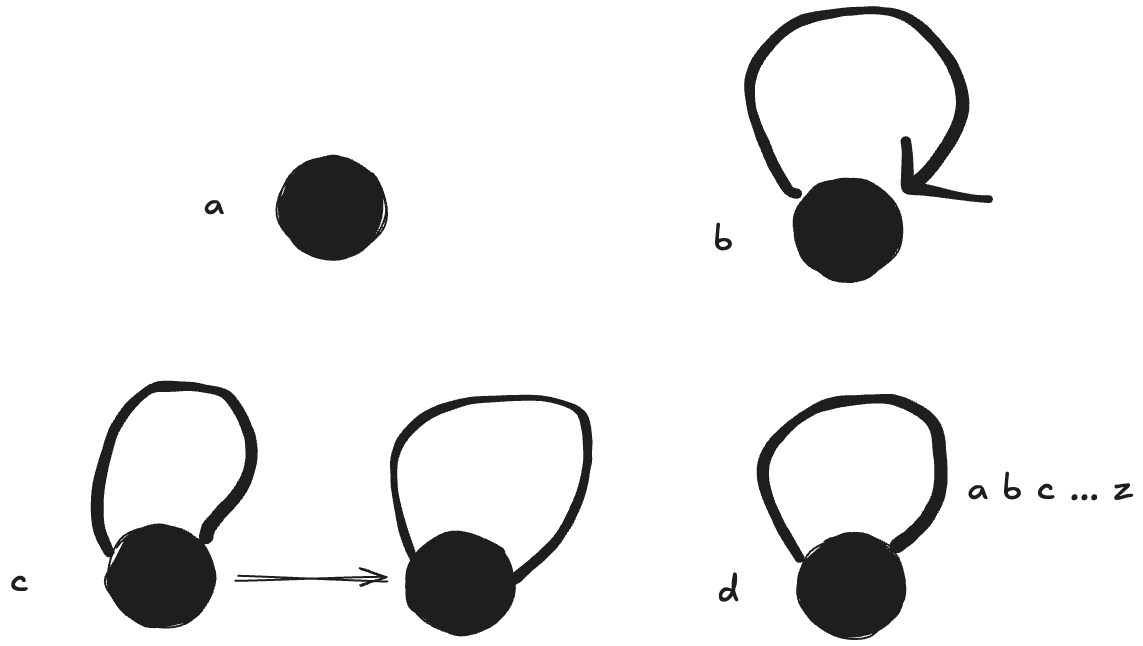
Graphs

  • (a) is not a category since it needs at least a loop edge to represent the identity morphism.
  • (b) is just a single object with an identity morphism.
  • (c) is two objects, each with an identity morphism, with a morphism going between them.
  • (d) is a monoid, i.e. a category with an associative binary operation (composition of morphisms) and an identity “element” (an identity morphism which we can arbitrarily say is one of the 26).
2. What kind of order is this? (a) A set of sets with the inclusion relation: A is included in B if every element of A is also an element of B. (b) C++ types with the following subtyping relation: T1 is a subtype of T2 if a pointer to T1 can be passed to a function that expects a pointer to T2 without triggering a compilation error.

  • (a) is a partial order. The relation is reflexive because every set is inclusive of its own elements, antisymetric because if B is inclusive of A then A cannot be inclusive of B (unless A and B are the same set) and transitive because if C is inclusive of B and B is inclusive of A, then C must be inclusive of A. (a) is not a total order because two sets A and B can have little or nothing in common such that they aren’t in an inclusion relation.
  • (b) is a preorder. The relation is reflexive because every type by the given definition is a subtype of itself, transitive because if T1 is a subtype of T2 and T2 is a subtype of T3 then T1 must be subtype of T3, but not antisymetric because distinct type specifiers (e.g. short int & signed short) for the same effective type in the relation constitute symmetry.

3. Considering that Bool is a set of two values True and False, show that it forms two (set-theoretical) monoids with respect to operator && (AND) and || (OR).

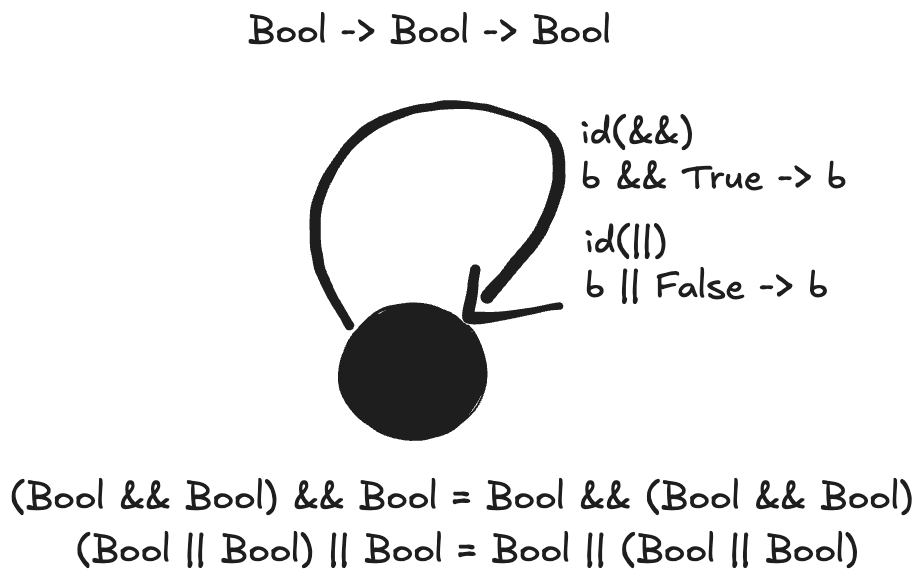
Bool Monoids

  • Closure: Both && and || are binary operations that take two booleans and return a boolean.
  • Identity:
    • The identity of && is True. When given as an operand the operation will always return what the other operand is.
    • The identity of || is False. When given as an operand the operation will always return what the other operand is.
  • Associativity:
    • For &&, the inclusion of False in a composition will result in an output of False. The non-inclusion of False will result in an output of True.
    • For ||, the inclusion of True in a composition will result in an output of True. The non-inclusion of True will result in an output of False.

4. Represent the Bool monoid with the AND operator as a category: List the morphisms and their rules of composition.

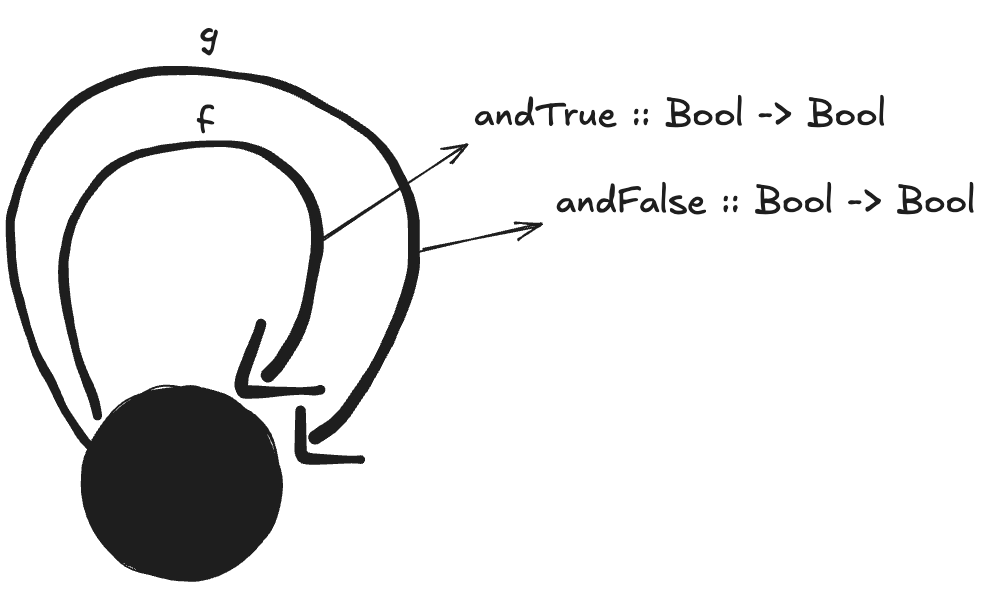
Bool Monoid as Category

  • f is a morphism andTrue which takes a Bool as input and does the && operation on it with True.
  • g is a morphism andFalse which takes a Bool as input and does the && operation on it with False.
  • The two morphisms compose to give morphisms of andTrue andFalse, andFalse andTrue andFalse… etc.

5. Represent addition modulo 3 as a monoid category.

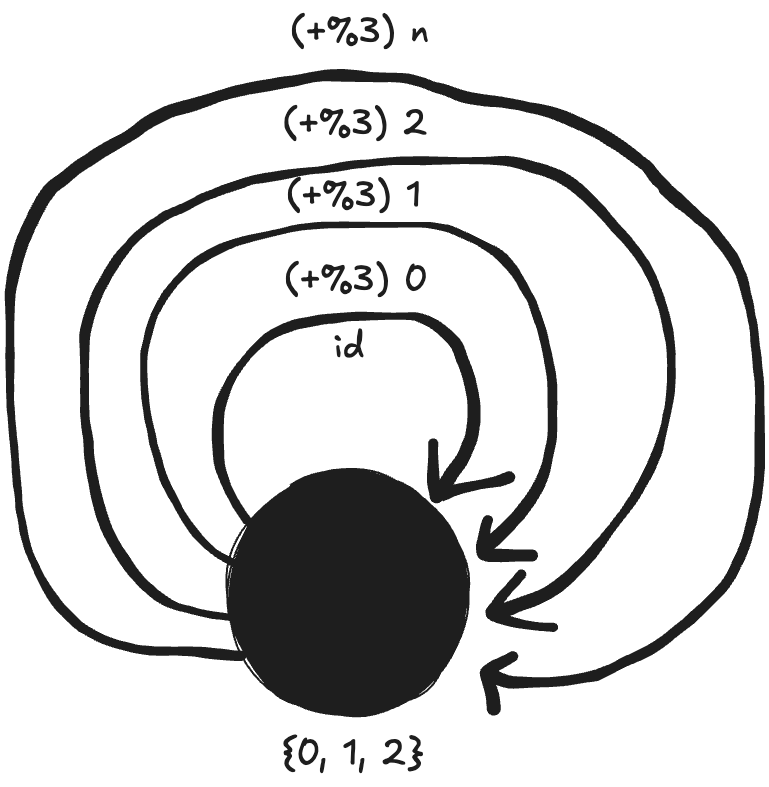
Addition Modulo 3

  • For there to be an identity morphism ((+%3) 0) the object must be the set: {0, 1, 2}, since no integer greater than 2 can be returned from a mod 3 operation.
  • Associativity:
    • (a + b) + c = d (mod 3) and a + (b + c) = d (mod 3)
    • e.g. (1 + 20) + 27 = 0 (mod 3) and 1 + (20 + 27) = 0 (mod 3)