An Introduction to Functional Programming Through Lambda Calculus

In one of Richard Gabriel’s essays about programming he writes about abstraction and makes a comparison between the compressing effect of abstraction in programming and the compression of meaning in a line of poetry. These exercises cover just the basics of Lambda Calculus, but you do get the sense when working through them of how it captures everything computable and compresses it all down into a few simple concepts.

Exercise 2.1

Analyse each of the following λ expressions to clarify its structure. If the expression is a function, identify the bound variable and the body expression, and then analyse the body expression. If the expression is an application, identify the function and argument expressions, and then analyse the function and argument expressions.

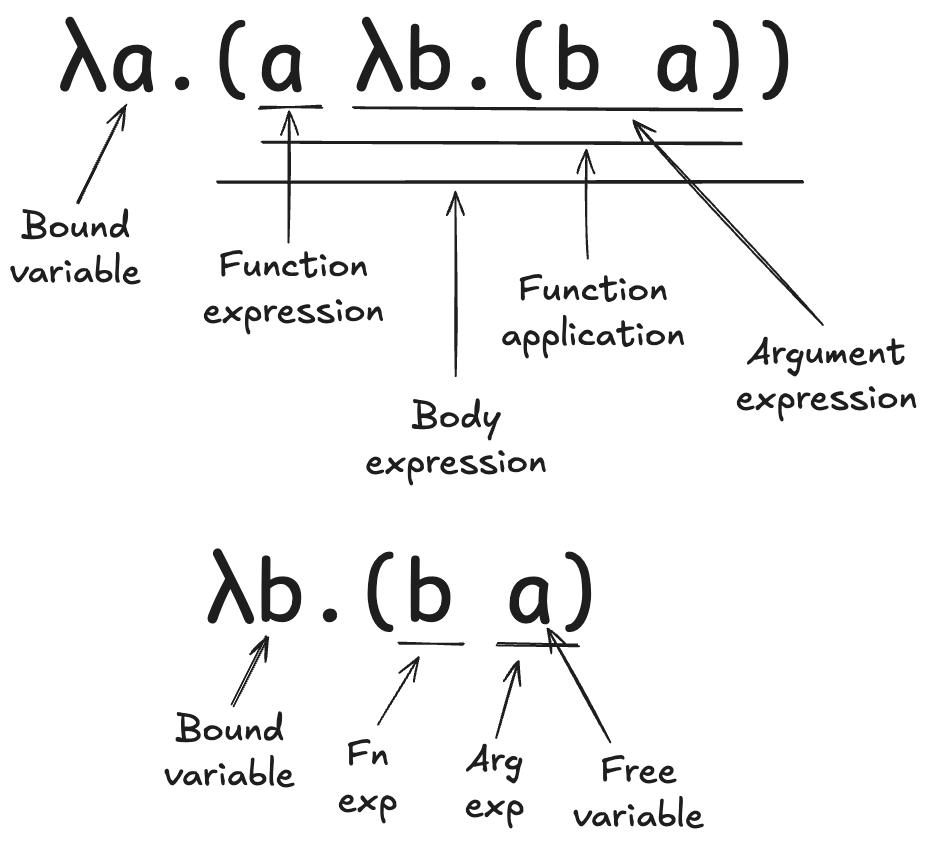
(a) λa.(a λb.(b a))

(b) λx.λy.λz.((z x) (z y))

• Bound variable: x
• Body expression: λy.λz.((z x) (z y))
  • Bound variable: y
  • Body expression: λz.((z x) (z y))
    • Bound variable: z
    • Body expression: ((z x) (z y))
      • Function expression: (z x)
        • Function expression: z
        • Argument expression: x
      • Argument expression: (z y)
        • Function expression: z
        • Argument expression: y

(c) (λf.λg.(λh.(g h) f) λp.λq.p)

• Function expression: λf.λg.(λh.(g h) f)
  • Bound variable: f
  • Body expression: λg.(λh.(g h) f)
    • Bound variable: g
    • Body expression: (λh.(g h) f)
      • Function expression: λh.(g h)
        • Bound variable: h
        • Body expression: (g h)
          • Function expression: g
          • Argument expression: h
      • Argument expression: f
• Argument expression: λp.λq.p
  • Bound variable: p
  • Body expression: λq.p
    • Bound variable: q
    • Body expression: p

(d) λfee.λfi.λfo.λfum.(fum (fo (fi fee)))

• Bound variable: fee
• Body expression: λfi.λfo.λfum.(fum (fo (fi fee)))
  • Bound variable: fi
  • Body expression: λfo.λfum.(fum (fo (fi fee)))
    • Bound variable: fo
    • Body expression: λfum.(fum (fo (fi fee)))
      • Bound variable: fum
      • Body expression: (fum (fo (fi fee)))
        • Function expression: fum
        • Argument expression: (fo (fi fee))
          • Function expression: fo
          • Argument expression: (fi fee)
            • Function expression: fi
            • Argument expression: fee

(e) (λp.(λq.p λx.(x p)) λi.λj.(j i))

• Function expression: λp.(λq.p λx.(x p))
  • Bound variable: p
  • Body expression: (λq.p λx.(x p))
    • Function expression: λq.p
      • Bound variable: q
      • Body expression: p
    • Argument expression: λx.(x p)
      • Bound variable: x
      • Body expression: (x p)
        • Function expression: x
        • Argument expression: p
• Argument expression: λi.λj.(j i)
  • Bound variable: i
  • Body expression: λj.(j i)
    • Bound variable: j
    • Body expression: (j i)
      • Function expression: j
      • Argument expression: i

Exercise 2.2

Evaluate the following λ expressions:

(a) ((λx.λy.(y x) λp.λq.p) λi.i)

Evaluates to the select_first function which stores the first argument, discards the second then returns the first.

=> ((λx.λy.(y x) λp.λq.p) λi.i)
=> (λy.(y λp.λq.p) λi.i)
=> (λi.i λp.λq.p)
=> λp.λq.p

(b) (((λx.λy.λz.((x y) z) λf.λa.(f a)) λi.i) λj.j)

Evaluates to the identity function.

=> (((λx.λy.λz.((x y) z) λf.λa.(f a)) λi.i) λj.j)
=> ((λy.λz.((λf.λa.(f a) y) z) λi.i) λj.j)
=> (λz.((λf.λa.(f a) λi.i) z) λj.j)
=> ((λf.λa.(f a) λi.i) λj.j)
=> (λa.(λi.i a) λj.j)
=> (λi.i λj.j)
=> λj.j

(c) (λh.((λa.λf.(f a) h) h) λf.(f f))

Evaluates to the self_apply function applied to itself and so it never terminates.

=> (λh.((λa.λf.(f a) h) h) λf.(f f))
=> ((λa.λf.(f a) λf.(f f)) λf.(f f))
=> (λf.(f λf.(f f)) λf.(f f))
=> (λf.(f f) λf.(f f))
=> (λf.(f f) λf.(f f))
=> ...

(d) ((λp.λq.(p q) (λx.x λa.λb.a)) λk.k)

Evaluates to a function that takes an argument and simply returns the identity function.

=> ((λp.λq.(p q) (λx.x λa.λb.a)) λk.k)
=> ((λp.λq.(p q) λa.λb.a)) λk.k)
=> (λq.(λa.λb.a q) λk.k)
=> (λa.λb.a λk.k)
=> λb.λk.k

(e) (((λf.λg.λx.(f (g x)) λs.(s s)) λa.λb.b) λx.λy.x)

Evaluates to the identity function.

=> (((λf.λg.λx.(f (g x)) λs.(s s)) λa.λb.b) λx.λy.x)
=> ((λg.λx.(λs.(s s) (g x)) λa.λb.b) λx.λy.x)
=> (λx.(λs.(s s) (λa.λb.b x)) λx.λy.x)
=> (λs.(s s) (λa.λb.b λx.λy.x))
=> (λs.(s s) (λb.b))
=> (λb.b λb.b)
=> λb.b

Exercise 2.3

For each of the following pairs, show that function (i) is equivalent to the function resulting from expression (ii) by applying both to arbitrary arguments:

(a)(i) identity

(identity <arg>) => <arg>

(a)(ii) (apply (apply identity))

=> (apply (apply identity))
=> (λf.λa.(f a) (λf.λa.(f a) λx.x))
=> (λf.λa.(f a) λa.(λx.x a))
=> (λa.(λa.(λx.x a) a))
=> λa.(λx.x a)
=> λa.a

(λa.a <arg>) => <arg>

(b)(i) apply

((apply <arg1>) <arg2>) => (<arg1> <arg2>)

(b)(ii) λx.λy.(((make_pair x) y) identity)

=> λx.λy.(((make_pair x) y) identity)
=> λx.λy.(((make_pair x) y) λa.a)
=> λx.λy.(((λfst.λsnd.λfn.((fn fst) snd) x) y) λa.a)
=> λx.λy.((λsnd.λfn.((fn x) snd) y) λa.a)
=> λx.λy.(λfn.((fn x) y) λa.a)
=> λx.λy.((λ.a.a x) y)
=> λx.λy.(x y)

(λx.λy.(x y) <arg1> <arg2> => (<arg1> <arg2>)

(c)(i) identity

(identity <arg>) => <arg>

(c)(ii) (self_apply (self_apply select_second))

=> (self_apply (self_apply select_second))
=> (self_apply (self_apply λfst.λsnd.snd))
=> (λs.(s s) (λs.(s s) λfst.λsnd.snd))
=> (λs.(s s) (λfst.λsnd.snd λfst.λsnd.snd))
=> (λs.(s s) (λsnd.snd))
=> (λsnd.snd λsnd.snd)
=> λsnd.snd

(λsnd.snd <arg>) => <arg>

Exercise 2.4

Define a function def make_triplet = ... which is like make_pair but constructs a triplet from a sequence of three arguments so that any one of the arguments may be selected by the subsequent application of a triplet to a selector function.

Define selector functions def triplet_first = ..., def triplet_second = ... and def triplet_third = ... which will select the first, second or third item from a triplet respectively.

Show that:

make_triplet <item1> <item2> <item3> triplet_first => ... => <item1> make_triplet <item1> <item2> <item3> triplet_second => ... => <item2> make_triplet <item1> <item2> <item3> triplet_third => ... => <item3>

make_triplet

def make_triplet = λx.λy.λz.λfn.(((fn x) y) z)

Selectors

def triplet_first = λfst.λsnd.λthd.fst
def triplet_second = λfst.λsnd.λthd.snd
def triplet_third = λfst.λsnd.λthd.thd

Demonstrations

triplet_first

=> ((((make_triplet <i1>) <i2>) <i3>) triplet_first)
=> ((((make_triplet <i1>) <i2>) <i3>) λfst.λsnd.λthd.fst)
=> ((((λx.λy.λz.λfn.(((fn x) y) z) <i1>) <i2>) <i3>) λfst.λsnd.λthd.fst)
=> (((λy.λz.λfn.(((fn i1) y) z) <i2>) <i3>) λfst.λsnd.λthd.fst)
=> ((λz.λfn.(((fn i1) i2) z) <i3>) λfst.λsnd.λthd.fst)
=> ((λfn.(((fn i1) i2) i3) λfst.λsnd.λthd.fst)
=> (((λfst.λsnd.λthd.fst i1) i2) i3)
=> ((λsnd.λthd.i1 i2) i3)
=> (λthd.i1 i3)
=> i1

triplet_second

=> ((((make_triplet <i1>) <i2>) <i3>) triplet_second)
=> ((((make_triplet <i1>) <i2>) <i3>) λfst.λsnd.λthd.snd)
=> ...
=> (((λfst.λsnd.λthd.snd i1) i2) i3)
=> ((λsnd.λthd.snd i2) i3)
=> (λthd.i2 i3)
=> i2

triplet_third

=> ((((make_triplet <i1>) <i2>) <i3>) triplet_third)
=> ((((make_triplet <i1>) <i2>) <i3>) λfst.λsnd.λthd.thd)
=> ...
=> (((λfst.λsnd.λthd.thd i1) i2) i3)
=> ((λsnd.λthd.thd i2) i3)
=> (λthd.thd i3)
=> i3

Exercise 2.5

Analyse each of the following λ expressions to identify its free and bound variables, and those in its subexpressions:

(a) λx.λy.(λx.y λy.x)

λx.λy.(λx.y λy.x): Bound are all x and y.
(λx.y λy.x): Bound are first x and second y. Free are the other x and y.

(b) λx.(x (λy.(λx.x y) x))

λx.(x (λy.(λx.x y) x)): Bound are all x and y.
(x (λy.(λx.x y) x)): Bound are the second x, third x and all y. Free are the first x and last x.
(λy.(λx.x y) x): Bound are the first x, second x and all y. Free is the last x.
((λx.x y) x): Bound are the first x and second x. Free are the y and last x.

(c) λa.(λb.a λb.(λa.a b))

λa.(λb.a λb.(λa.a b)): Bound are all a and b.
(λb.a λb.(λa.a b)): Bound are all b and the second and third a. Free is the first a.
λb.a: Bound is b. Free is a.
λb.(λa.a b): Bound are all a and b.
(λa.a b): Bound is a. Free is b.

(d) (λfree.bound λbound.(λfree.free bound))

(λfree.bound λbound.(λfree.free bound)): Bound are all free and the second and third bound. Free is the first bound.
λbound.(λfree.free bound): Are variable are bound.
(λfree.free bound): Bound are all free. Free is bound.

(e) λp.λq.(λr.(p (λq.(λp.(r q)))) (q p))

λp.λq.(λr.(p (λq.(λp.(r q)))) (q p)): Bound are all p, q and r.
λq.(λr.(p (λq.(λp.(r q)))) (q p)): Bound are all q and r. Free are the first and last p.
(λr.(p (λq.(λp.(r q)))) (q p)): Bound are all r and the second and third q . Free are the first and last p and the last q.
λr.(p (λq.(λp.(r q)))): Bound are all r, all q and the second p. Free is the first p.
(p (λq.(λp.(r q)))): Bound are all q and the second p. Free are the first p and the r.
λq.(λp.(r q)): Bound are all q and p. Free is the r.
λp.(r q): Bound is p. Free are r and q.

Exercise 2.6

Use α conversion to ensure unique names in the expressions in Exercise 2.5 above.

(a) λx.λy.(λx.y λy.x)

λx.λy.(λa.y λb.x)

(b) λx.(x (λy.(λx.x y) x))

λx.(x (λy.(λa.a y) x))

(c) λa.(λb.a λb.(λa.a b))

λa.(λb.a λx.(λy.y x))

(d) (λfree.bound λbound.(λfree.free bound))

(λa.b λc.(λd.d c))

(e) λp.λq.(λr.(p (λq.(λp.(r q)))) (q p))

λp.λq.(λr.(p (λs.(λt.(r s)))) (q p))