Over the past few months I’ve had an interest in functional programming. This has brought me to category theory and abstract algebra and for me the latter subject has really shone a light on the former; in particular I found that in Lara Alcock’s book How to Think About Abstract Algebra she very helpfully explains that there are broadly three approaches to teaching the subject: formal, equation solving and geometric. The formal approach of working mainly with the abstract concepts I’ve found to be common in explanations of category theory and I was missing something concise from the equation solving or geometric approach to show more clearly what is being abstracted over. From Alcock’s book I gained a clearer intution of the structure that abstract algebra and category theory are getting at (e.g. the structure that many programming solutions exist within) that I benefited from when returning to learn about category theory.

Natural Transformations

Bartosz Milewski’s video on Natural Transformations was excellent for understanding this concept. The below diagram illustrates the common structure of something very normal in programming, which is to do basically the same thing within varying contexts.

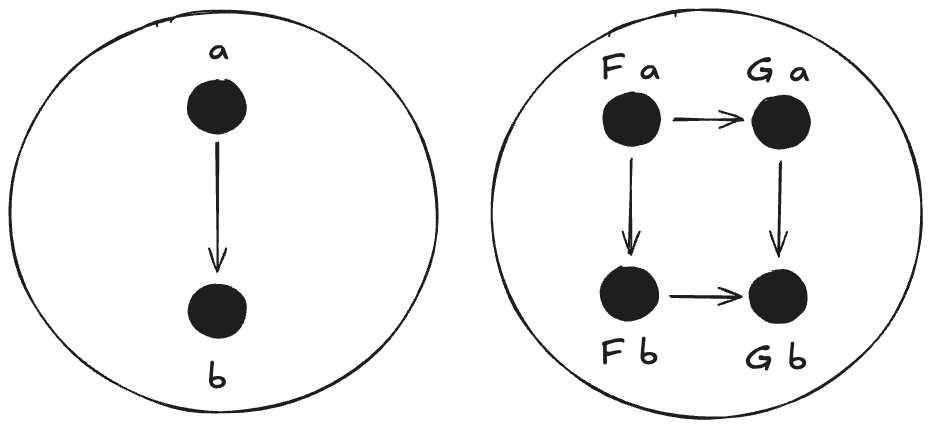
Formally the diagram shows a Natural Transformation, which is the mapping of one Functor to another where a Functor is a mapping from one category or sub-category to another. Concretely:

• a can be substituted for int
• b can be substituted for string
• F can be substituted for List
• G can be substituted for Tree

The diagram is then a depiction of how a function from an int to a string has concommitant functions from list of ints to list of strings and tree of ints to tree of strings. These two functions map to each other insofar as a list of ints can be transformed to a tree of strings either by changing the container from list to tree then the contents from int to string, or by changing the contents from int to string and then the container from list to tree.

What is helpful about this formalisation is the reduction in program complexity by virtue of understanding that operations done on primitive types are essentially the same as operations done on a variety of more complex types, and that these types can be reached naturally through one another. This compression leaves room for programs to become more complex is ways that are beneficial to some goal.